Tema 4.1 Series De Potencias Definicion
A la suma de una sucesión de términos se denomina SERIE y el valor de dicha
suma, si es que tiene alguno, se define como
En efecto, al sumar suficientes terminos de la serie podemos aproximar las sumas parciales a 1 tanto como queramos Por consiguiente, parece razonable decir que la suma de esta serie infinita es 1
Estas sumas parciales forman una nueva sucesión, {s,n} , que puede o no tener límite.
Si
existe (como número finito), entonces, igual que en el éjemplo anterior, decimos ue es la suma de la serie infinita 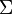 a,n..
a,n..
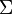 a,n..
a,n..
siendo "S" una forma de aproximarnos a un numero calculado mediante las Suma 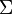 del "n"esimo termino de dicha serie.
del "n"esimo termino de dicha serie.
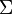 del "n"esimo termino de dicha serie.
del "n"esimo termino de dicha serie.
por tanto cuando escribimos
a,n= s queremos decir que si se suma una cantidad suficiente de términos de la serie, nos podemos acercar todo lo queramos al número "s". Observe que




No hay comentarios:
Publicar un comentario