Se
puede aplicar la ecuación de las series de Taylor como más sencillo le
resulte a cada quien, una de tantas formas la explicare aquí.
Lo primero que se hace es derivar unas 3 o 4 veces la función, esto
porque algunas funciones empiezan a tener un patrón repetitivo después
de cierto número de derivaciones, como la función e.
Después se tiene que sustituir "a" en cada una de las derivadas, pero
como se decidió que "a" era 0 se sustituye un 0 en cada derivada y se
observa que resultados da.
Esto
de sustituir en cada derivada es solo para simplificar la ecuación de
la serie y para darnos una idea de como se comporta la función. Una vez
que se tiene una idea del comportamiento de la función se puede ir
empezando a armar la ecuación de la serie
La serie de Taylor de una función f de numeros reales que es infinitamente diferenciable en un conjunto de números reales o complejos a, es la serie de potencias:

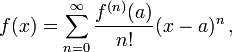
No hay comentarios:
Publicar un comentario