El número R se denomina radio de convergencia de la serie
Por convención, el radio de convergencia es R = O en el caso
El intervalo de convergencia de una serie de potencias consta de todos
para los cuales la serie converge.
En donde el intervalo es (—oo, +oo).
la desigualdad |x-a| - R
Donde Cualquier x es un punto extra,
(esto es, x = a ± R) puede suceder cualquier cosa: la serie puede converger para
ambos puntos extremos o divergir en ellos.
Un Ejemplo Muy claro de esto es el calculo del Numero e
que al igual que pi, es una serie infinita de teminos, pero que se calcula con la serie:

y como "x" pertenece a todos los reales, pues tiene un radio de convergencia infinito, ya que su dominio de dicha "x", es E (R).






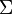





 . Formemos la serie de valores absolutos, es decir
. Formemos la serie de valores absolutos, es decir
 que no necesariamente
es de términos positivos.
que no necesariamente
es de términos positivos. la estudiaremos con
el criterio de D'Alembert, o sea si
la estudiaremos con
el criterio de D'Alembert, o sea si

 ó
ó  es
es  y el
y el